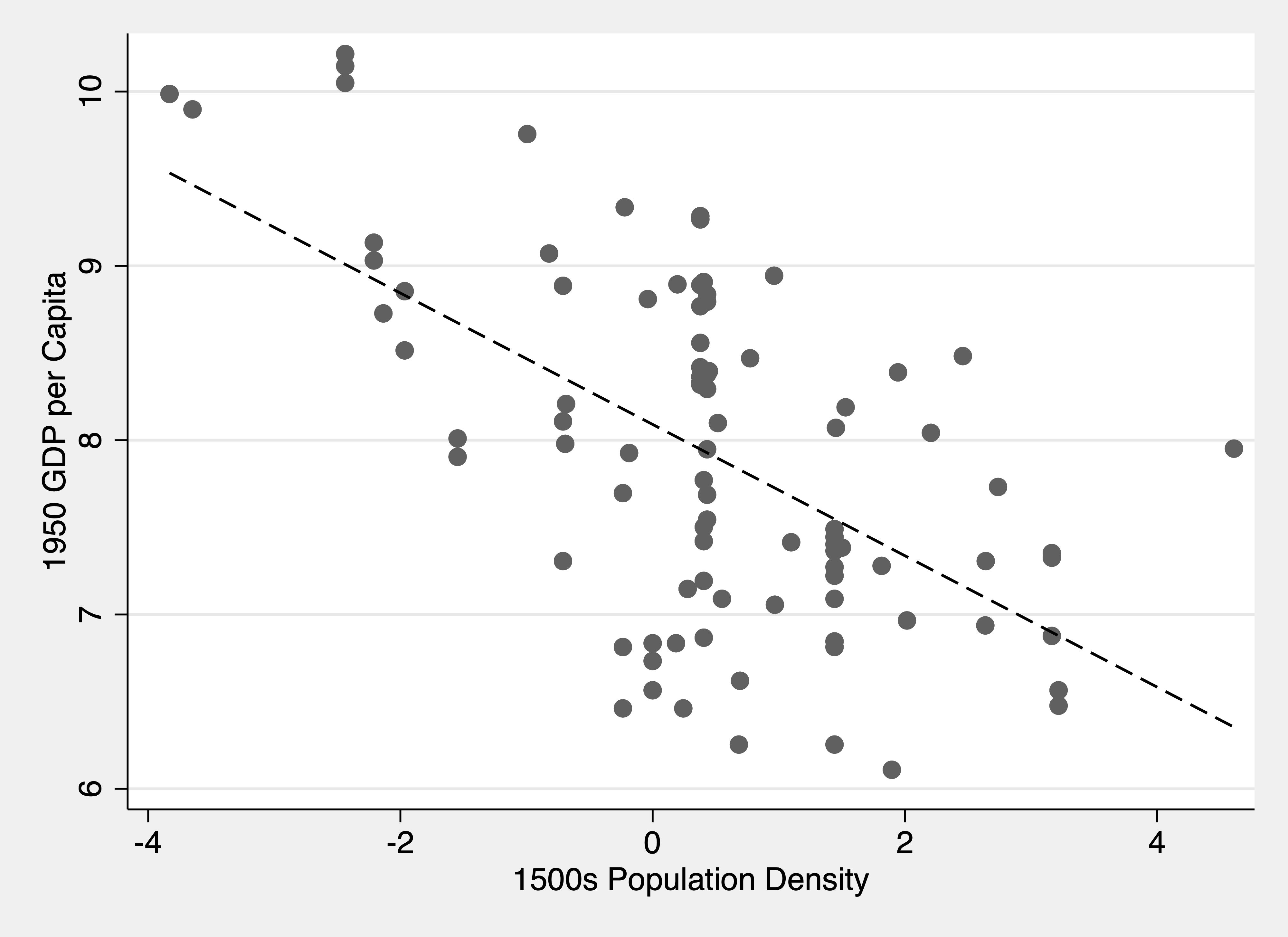
The Best Fit Regression Line
Start fresh ...
clear allReversal of Fortune: Geography and Institutions in the Making of the Modern World Income Distribution.. Daron Acemoglu, Simon Johnson, and James A. Robinson. Quarterly Journal of Economics, 117, November 2002: pp. 1231-1294.,
In this 2002 article, Acemoglu, Johnson, and Robinson argue that countries that were more wealthy and urbanized in the 1500s saw their fortunes reverse in the subsequent centuries. Countries such as Rwanda and Tanzania were high-density areas in the 1500s but in the 20th century had low GDP per capita. The authors argue that this is because European colonialism settled more in areas that were less developed in the 1500s, but then went on to become strong economies. A simple bivariate relationship motivates their argument.
. use reversal.dta, clear
. describe
Contains data from reversal.dta
obs: 91
vars: 10 26 Nov 2018 22:42
size: 7,553
───────────────────────────────────────────────────────────────────────────────────────────
storage display value
variable name type format label variable label
───────────────────────────────────────────────────────────────────────────────────────────
countryn str20 %-9s Country Name
shortnam str3 %-9s Country Name
logpgp95 double %10.0g Log GDP per Capita in 1995
logem4 double %10.0g
urbz1995 double %10.0g Urbanization in 1995 (Proportion Population
in Large Towns)
lpd1500s double %10.0g Log Population Density 1500s
cu1500 double %10.0g Urbanization in 1000s (Chandler)
sjb1500 double %10.0g Urbanization in 1500s (Bairoch)
sjb1000 double %10.0g Urbanization in 1000s (Bairoch)
continent long %8.0g continent
───────────────────────────────────────────────────────────────────────────────────────────
Sorted by:
Use the regress or reg command to run a regression.
. regress logpgp95 lpd1500s
Source │ SS df MS Number of obs = 91
─────────────┼────────────────────────────────── F(1, 89) = 46.12
Model │ 30.3661927 1 30.3661927 Prob > F = 0.0000
Residual │ 58.5990948 89 .658416795 R-squared = 0.3413
─────────────┼────────────────────────────────── Adj R-squared = 0.3339
Total │ 88.9652874 90 .988503194 Root MSE = .81143
─────────────┬────────────────────────────────────────────────────────────────
logpgp95 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lpd1500s │ -.3766786 .0554659 -6.79 0.000 -.4868881 -.266469
_cons │ 8.090425 .0887273 91.18 0.000 7.914126 8.266725
─────────────┴────────────────────────────────────────────────────────────────
In a simple regression, a scatter plot can show the data cleanly
. twoway scatter logpgp95 lpd1500s || lfit logpgp95 lpd1500s, /// > ytitle(1950 GDP per Capita) /// > xtitle(1500s Population Density) /// > legend(off) . graph export reversal_fit.png, width(2000) replace (file reversal_fit.png written in PNG format)

The Best Fit Regression Line
Different options:
. regress logpgp95 lpd1500s, beta
Source │ SS df MS Number of obs = 91
─────────────┼────────────────────────────────── F(1, 89) = 46.12
Model │ 30.3661927 1 30.3661927 Prob > F = 0.0000
Residual │ 58.5990948 89 .658416795 R-squared = 0.3413
─────────────┼────────────────────────────────── Adj R-squared = 0.3339
Total │ 88.9652874 90 .988503194 Root MSE = .81143
─────────────┬────────────────────────────────────────────────────────────────
logpgp95 │ Coef. Std. Err. t P>|t| Beta
─────────────┼────────────────────────────────────────────────────────────────
lpd1500s │ -.3766786 .0554659 -6.79 0.000 -.5842314
_cons │ 8.090425 .0887273 91.18 0.000 .
─────────────┴────────────────────────────────────────────────────────────────
Multiple regression -- add more terms.
. reg logpgp95 lpd1500s sjb1000
Source │ SS df MS Number of obs = 34
─────────────┼────────────────────────────────── F(2, 31) = 21.66
Model │ 14.2886648 2 7.1443324 Prob > F = 0.0000
Residual │ 10.2267689 31 .329895772 R-squared = 0.5828
─────────────┼────────────────────────────────── Adj R-squared = 0.5559
Total │ 24.5154337 33 .742891931 Root MSE = .57437
─────────────┬────────────────────────────────────────────────────────────────
logpgp95 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lpd1500s │ -.321548 .0551574 -5.83 0.000 -.4340423 -.2090538
sjb1000 │ -.0031051 .0284966 -0.11 0.914 -.0612242 .055014
_cons │ 8.642748 .1485872 58.17 0.000 8.339703 8.945794
─────────────┴────────────────────────────────────────────────────────────────
What if explanatory variable is a categorical?
. tab continent
continent │ Freq. Percent Cum.
────────────┼───────────────────────────────────
Africa │ 45 49.45 49.45
Americas │ 32 35.16 84.62
Asia │ 12 13.19 97.80
Oceania │ 2 2.20 100.00
────────────┼───────────────────────────────────
Total │ 91 100.00
. reg logpgp95 lpd1500s sjb1000 continent
Source │ SS df MS Number of obs = 34
─────────────┼────────────────────────────────── F(3, 30) = 13.97
Model │ 14.2889201 3 4.76297337 Prob > F = 0.0000
Residual │ 10.2265136 30 .340883787 R-squared = 0.5829
─────────────┼────────────────────────────────── Adj R-squared = 0.5411
Total │ 24.5154337 33 .742891931 Root MSE = .58385
─────────────┬────────────────────────────────────────────────────────────────
logpgp95 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lpd1500s │ -.3212955 .0568227 -5.65 0.000 -.437343 -.205248
sjb1000 │ -.0028831 .0300819 -0.10 0.924 -.0643186 .0585524
continent │ .0041495 .1516197 0.03 0.978 -.3054991 .3137982
_cons │ 8.632706 .3968173 21.75 0.000 7.822297 9.443115
─────────────┴────────────────────────────────────────────────────────────────
(what's wrong with this?)
. reg logpgp95 lpd1500s sjb1000 i.continent
Source │ SS df MS Number of obs = 34
─────────────┼────────────────────────────────── F(5, 28) = 11.84
Model │ 16.6431982 5 3.32863964 Prob > F = 0.0000
Residual │ 7.87223551 28 .281151268 R-squared = 0.6789
─────────────┼────────────────────────────────── Adj R-squared = 0.6215
Total │ 24.5154337 33 .742891931 Root MSE = .53024
─────────────┬────────────────────────────────────────────────────────────────
logpgp95 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lpd1500s │ -.4108716 .0664944 -6.18 0.000 -.5470792 -.2746641
sjb1000 │ .017904 .0287151 0.62 0.538 -.0409162 .0767241
│
continent │
Americas │ -.9076474 .3537367 -2.57 0.016 -1.632244 -.1830505
Asia │ -.5490911 .3531067 -1.56 0.131 -1.272397 .1742151
Oceania │ -.3875177 .548546 -0.71 0.486 -1.511163 .7361279
│
_cons │ 9.260819 .3231567 28.66 0.000 8.598863 9.922776
─────────────┴────────────────────────────────────────────────────────────────
Create a new variable in dataset
. reg logpgp95 lpd1500s sjb1000 i.continent
Source │ SS df MS Number of obs = 34
─────────────┼────────────────────────────────── F(5, 28) = 11.84
Model │ 16.6431982 5 3.32863964 Prob > F = 0.0000
Residual │ 7.87223551 28 .281151268 R-squared = 0.6789
─────────────┼────────────────────────────────── Adj R-squared = 0.6215
Total │ 24.5154337 33 .742891931 Root MSE = .53024
─────────────┬────────────────────────────────────────────────────────────────
logpgp95 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lpd1500s │ -.4108716 .0664944 -6.18 0.000 -.5470792 -.2746641
sjb1000 │ .017904 .0287151 0.62 0.538 -.0409162 .0767241
│
continent │
Americas │ -.9076474 .3537367 -2.57 0.016 -1.632244 -.1830505
Asia │ -.5490911 .3531067 -1.56 0.131 -1.272397 .1742151
Oceania │ -.3875177 .548546 -0.71 0.486 -1.511163 .7361279
│
_cons │ 9.260819 .3231567 28.66 0.000 8.598863 9.922776
─────────────┴────────────────────────────────────────────────────────────────
. predict yhat
(option xb assumed; fitted values)
(57 missing values generated)
. summarize logpgp95 yhat
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
logpgp95 │ 91 7.918999 .994235 6.109248 10.21574
yhat │ 34 8.614128 .7101685 7.443351 10.37231
Or residuals
. predict residuals, residuals
(57 missing values generated)
.
. summarize logpgp95 yhat residuals
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
logpgp95 │ 91 7.918999 .994235 6.109248 10.21574
yhat │ 34 8.614128 .7101685 7.443351 10.37231
residuals │ 34 -2.74e-09 .4884185 -1.083866 .8918947
Instead of copy-pasting Stata output, use designated commands:
. reg logpgp95 lpd1500s sjb1000
Source │ SS df MS Number of obs = 34
─────────────┼────────────────────────────────── F(2, 31) = 21.66
Model │ 14.2886648 2 7.1443324 Prob > F = 0.0000
Residual │ 10.2267689 31 .329895772 R-squared = 0.5828
─────────────┼────────────────────────────────── Adj R-squared = 0.5559
Total │ 24.5154337 33 .742891931 Root MSE = .57437
─────────────┬────────────────────────────────────────────────────────────────
logpgp95 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lpd1500s │ -.321548 .0551574 -5.83 0.000 -.4340423 -.2090538
sjb1000 │ -.0031051 .0284966 -0.11 0.914 -.0612242 .055014
_cons │ 8.642748 .1485872 58.17 0.000 8.339703 8.945794
─────────────┴────────────────────────────────────────────────────────────────
. esttab
────────────────────────────
(1)
logpgp95
────────────────────────────
lpd1500s -0.322***
(-5.83)
sjb1000 -0.00311
(-0.11)
_cons 8.643***
(58.17)
────────────────────────────
N 34
────────────────────────────
t statistics in parentheses
* p<0.05, ** p<0.01, *** p<0.001
.
. eststo clear // clear estimated tables
. eststo: reg logpgp95 lpd1500s
Source │ SS df MS Number of obs = 91
─────────────┼────────────────────────────────── F(1, 89) = 46.12
Model │ 30.3661927 1 30.3661927 Prob > F = 0.0000
Residual │ 58.5990948 89 .658416795 R-squared = 0.3413
─────────────┼────────────────────────────────── Adj R-squared = 0.3339
Total │ 88.9652874 90 .988503194 Root MSE = .81143
─────────────┬────────────────────────────────────────────────────────────────
logpgp95 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lpd1500s │ -.3766786 .0554659 -6.79 0.000 -.4868881 -.266469
_cons │ 8.090425 .0887273 91.18 0.000 7.914126 8.266725
─────────────┴────────────────────────────────────────────────────────────────
(est1 stored)
. eststo: reg logpgp95 lpd1500s sjb1000
Source │ SS df MS Number of obs = 34
─────────────┼────────────────────────────────── F(2, 31) = 21.66
Model │ 14.2886648 2 7.1443324 Prob > F = 0.0000
Residual │ 10.2267689 31 .329895772 R-squared = 0.5828
─────────────┼────────────────────────────────── Adj R-squared = 0.5559
Total │ 24.5154337 33 .742891931 Root MSE = .57437
─────────────┬────────────────────────────────────────────────────────────────
logpgp95 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lpd1500s │ -.321548 .0551574 -5.83 0.000 -.4340423 -.2090538
sjb1000 │ -.0031051 .0284966 -0.11 0.914 -.0612242 .055014
_cons │ 8.642748 .1485872 58.17 0.000 8.339703 8.945794
─────────────┴────────────────────────────────────────────────────────────────
(est2 stored)
. eststo: reg logpgp95 lpd1500s sjb1000 i.continent
Source │ SS df MS Number of obs = 34
─────────────┼────────────────────────────────── F(5, 28) = 11.84
Model │ 16.6431982 5 3.32863964 Prob > F = 0.0000
Residual │ 7.87223551 28 .281151268 R-squared = 0.6789
─────────────┼────────────────────────────────── Adj R-squared = 0.6215
Total │ 24.5154337 33 .742891931 Root MSE = .53024
─────────────┬────────────────────────────────────────────────────────────────
logpgp95 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lpd1500s │ -.4108716 .0664944 -6.18 0.000 -.5470792 -.2746641
sjb1000 │ .017904 .0287151 0.62 0.538 -.0409162 .0767241
│
continent │
Americas │ -.9076474 .3537367 -2.57 0.016 -1.632244 -.1830505
Asia │ -.5490911 .3531067 -1.56 0.131 -1.272397 .1742151
Oceania │ -.3875177 .548546 -0.71 0.486 -1.511163 .7361279
│
_cons │ 9.260819 .3231567 28.66 0.000 8.598863 9.922776
─────────────┴────────────────────────────────────────────────────────────────
(est3 stored)
. esttab
────────────────────────────────────────────────────────────
(1) (2) (3)
logpgp95 logpgp95 logpgp95
────────────────────────────────────────────────────────────
lpd1500s -0.377*** -0.322*** -0.411***
(-6.79) (-5.83) (-6.18)
sjb1000 -0.00311 0.0179
(-0.11) (0.62)
1.continent 0
(.)
2.continent -0.908*
(-2.57)
3.continent -0.549
(-1.56)
4.continent -0.388
(-0.71)
_cons 8.090*** 8.643*** 9.261***
(91.18) (58.17) (28.66)
────────────────────────────────────────────────────────────
N 91 34 34
────────────────────────────────────────────────────────────
t statistics in parentheses
* p<0.05, ** p<0.01, *** p<0.001
With more formats (http://repec.org/bocode/e/estout/esttab.html)
. esttab, label b(2) se(a1) r2 ar2
────────────────────────────────────────────────────────────────────
(1) (2) (3)
Log GDP~1995 Log GDP~1995 Log GDP~1995
────────────────────────────────────────────────────────────────────
Log Population~1500s -0.38*** -0.32*** -0.41***
(0.06) (0.06) (0.07)
Urbanization in 10~) -0.00 0.02
(0.03) (0.03)
Africa 0.00
(.)
Americas -0.91*
(0.4)
Asia -0.55
(0.4)
Oceania -0.39
(0.5)
Constant 8.09*** 8.64*** 9.26***
(0.09) (0.1) (0.3)
────────────────────────────────────────────────────────────────────
Observations 91 34 34
R-squared 0.341 0.583 0.679
Adjusted R-squared 0.334 0.556 0.622
────────────────────────────────────────────────────────────────────
Standard errors in parentheses
* p<0.05, ** p<0.01, *** p<0.001